第2種スターリング数は「写像12相」と呼ばれるものを通して学ぶと、他の数え上げ問題との関わりが分かり全体像がスッキリします。ぜひ確認してみることをおすすめします。「写像12相」で典型的な数え上げ問題のパターン総整理 第2種スターリング数とは 第2種スターリング数 \(S(n,k)\) は高い回転数での運転は望めず,実用的なエンジン は成立しない。図2に示すように,スターリング エンジンは,温度差を持つ2 つのシリンダと約 90°の位相差を持つ2つのピストン,ヒータ・再 生器・クーラと呼ばれる熱交換器,さらに円滑なツインバードがスターリングクーラー事業に本腰――数年後には民生機に : 宇宙冷蔵庫、地上へ? » 14年07月30日 12時33分 公開 芹澤隆徳

ヤフオク F1440 レア 1piu1uguale3 Wolf S Head 美しい
スターリング 数学
スターリング 数学-また、設計によって数十度、あるいは数度の温度差でも動く低温度差型のエンジンを製作することが出来ます。温排水などの現在捨てられている熱を利用する 方法の一つになります。 4.スターリングエンジンの技術的課題 重さ大きさ(比出力)スターリング冷凍機は,蓄冷器を介して高温部(圧縮部)と低温部(膨張部)が配置され,圧縮ピストンと膨張ピスト ンは90 度の位相を保ちつつ駆動されるのが特徴である.図1に従い,その4 つの工程を説明する.なお,実際の各工程 は連続して行われて



ありゅ だるい 個人的にスターリングの公式の導出はlhaplusmethodを用いた方法も捺したい
スターリング数(スターリングすう、英 Stirling number )は、上昇階乗冪 (rising factorial) や 下降階乗冪 (falling factorial) を数値の冪乗と関係づけるための級数の展開係数として、イギリスの数学者 ジェームズ・スターリング (English版) が1730年に彼の著書 Methodus Differentialis で導入した数 である。著者梅谷 武 語句昇階乗,降階乗,第1種スターリング数,第2種スターリング数 作成 更新 44 スターリング数と冪和公式第1種スターリング数 s(n,k) の nが指定された表を計算します。
スターリング数 (Stirling number) は n 個の異なる球を m 個の同種の箱に分ける方法の数で、前項では 2 項係数の反転公式を用いて求めたが、包除原理を用いて求めることもできて ∵スターリング数は n 個の異なる球を m 個の同種 の箱に分ける方法の数なので、 m 個の異なる箱に分ける方法の数 S用のものではない.また後ほど登場する第2 種スターリング数との兼ね合いを考えると,上述のn とr につ いては逆にするか,あるいはQ(r,n) としたほうがよいのかもしれない.ここでは重複順列のnΠr にならっ て,そうしたわけである. 4/12スターリング数(スターリングすう、英 Stirling number )は、上昇階乗冪 (rising factorial) や 下降階乗冪 (falling factorial) を数値の冪乗と関係づけるための級数の展開係数として、イギリスの数学者 ジェームズ・スターリング (English版) が1730年に彼の著書 Methodus Differentialis で導入した数 である。
とスターリング数の閉じた式が求まる。 球が同種のときは、空箱があってよい条件での数 Y(n,m) は空箱がない条件下の数 X(nm,m) と等しい。 なぜなら X(nm,m) は、まず球を 1 個ずつ m 個の箱に入れておいて残り n 個を空箱ありで分ける方法の数 Y(n,m) と等しい。スターリング数 \( \newcommand{\stirlingI}{\genfrac{0pt}{}} % 第1種スターリング数 \newcommand{\stirlingII}{\genfrac\{\}{0pt}{}} % 第2種上記では、同一行の第2種スターリング数の総和という形でベル数を計算したが、ベル数 そのものを直接に計算する三角形も存在するようだ。 下記の三角形は、Aitken's array( A )から得られる。


スワドルデザインズ ウォッシュクロス3枚セット リトルラム スターリング Sdm 715st M Gift Hare ギフトハレ 通販 Yahoo ショッピング



00 号 スターリングエンジン発電装置用の回転数制御装置 Astamuse
第一種および第二種スターリング数と呼ばれる数列を定義して,その組合せ論的な意味付けを紹介します.参考とした本: Martin Aigner, A course in Enumeration, GTM 238, 07変数の昇冪 と降冪 を と定義します. 多項式の集合とはどちらもの基底だから,ある係数を使って,スターリング数には, 第1種スターリング数と第2種スターリング数があり, ともに, 組み合わせ論で意味をもつ数列です。 それらの数列は, 導入の時点では, 上昇階乗と下降階乗 (pdfファイル参照) と いう概念を用います。スターリングエンジン(英 Stirling engine )とは、熱機関の形式のひとつで、シリンダー内のガス(もしくは空気等)を外部から加熱・冷却し、その体積の変化(加熱による膨張・冷却による収縮)により仕事を得る外燃機関である 。 熱交換をすることによってカルノーサイクルと同じ理論効率と



第2種スターリング数 高校生向け 3 怜悧玲瓏 高校数学を天空から俯瞰する



Modern Slavery Act シャーマン アンド スターリング
スターリング数(スターリングすう、英 Stirling number )は、上昇階乗冪 (rising factorial) や 下降階乗冪 (falling factorial) を数値の冪乗と関係づけるための級数の展開係数として、イギリスの数学者 ジェームズ・スターリング (英語版) が1730年に彼の著書 Methodusスターリング冷凍機は,蓄冷器を介して高温部(圧縮部)と低温部(膨張部)が配置され,圧縮ピストンと膨張ピスト ンは90 度の位相を保ちつつ駆動されるのが特徴である.図1に従い,その4 つの工程を説明する.なお,実際の各工程 は連続して行われてSと回転数nと の関係及び作動ガスの相違と軸出力との関係が、妥当 に見積もられていなければならない。 3.実測値の整理法 著者らが、現在までに開発した高温度差形及び低温 度差形スターリングエンジンの性能特性試験を行い(10)



場合の数25 第2種スターリング数3 怜悧玲瓏 高校数学を天空から俯瞰する



書籍紹介詳細ページ
用のものではない.また後ほど登場する第2 種スターリング数との兼ね合いを考えると,上述のn とr につ いては逆にするか,あるいはQ(r,n) としたほうがよいのかもしれない.ここでは重複順列のnΠr にならっ て,そうしたわけである. 4/12スターリング数である. また,逆に x のベキ乗 xn をジョルダンの階乗記号によって n n n n n n k n k k n s (x ),0 ,1 1 , 0 ¦, と書いたときの snk, が第2 種のスターリング 数である.(「順列・組合せと確率」/山本幸一/岩波書店)スターリング数(スターリングすう、英 Stirling number )は、上昇階乗冪 (rising factorial) や 下降階乗冪 (falling factorial) を数値の冪乗と関係づけるための級数の展開係数として、イギリスの数学者 ジェームズ・スターリング (英語版) が1730年に彼の著書 Methodus



ありゅ だるい 個人的にスターリングの公式の導出はlhaplusmethodを用いた方法も捺したい



順列 組合せと確率 新装版 数学入門シリーズ 山本 幸一 本 通販 Amazon
スターリング数(スターリングすう、英 Stirling number )は、上昇階乗冪 (rising factorial) や 下降階乗冪 (falling factorial) を数値の冪乗と関係づけるための級数の展開係数として、イギリスの数学者 ジェームズ・スターリング (英語版) が1730年に彼の著書 Methodus Differentialis で導入した数 である。



何でもブログねた スターリング エンジン回転数測定 デジスコ撮影実習日誌



メルカリ フリーピストン スターリングエンジン おもちゃ ホビー グッズ 2 0 中古や未使用のフリマ
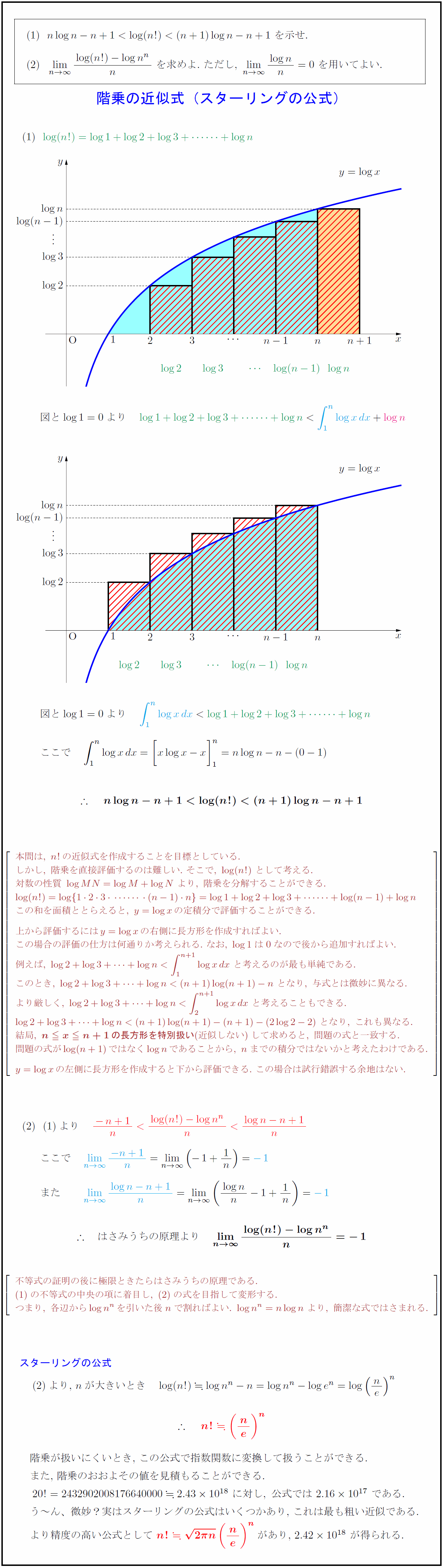


高校数学 階乗n の近似式 スターリングの公式 受験の月



3 D 英国ポンドスターリングのクマの罠 3dのストックフォトや画像を多数ご用意 Istock



Maison Margiela メゾンマルジェラ 11 エングレーブ スターリングシルバー シングルピアス Matchesfashion マッチズファッション



スターリングサインベクトルイラストのイラスト素材 ベクタ Image



基調講演 日本機械学会誌



メルカリ S T スターリング Mk 5 電動ガン トイガン 22 000 中古や未使用のフリマ



ヤフオク ヴァンガード スターリングウィッチ モモ Rrr 2



調和数 発散列 Wikipedia
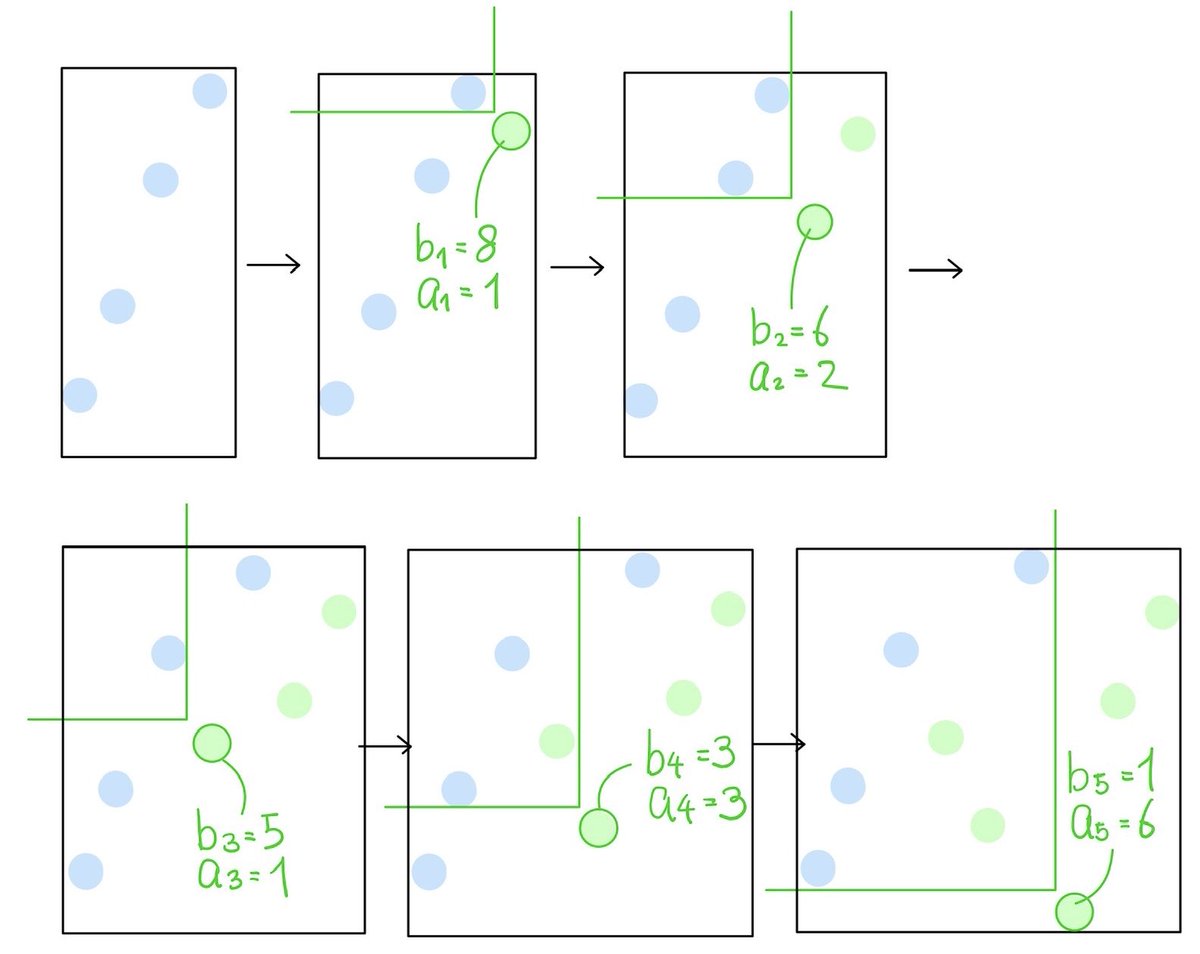


J80yxkfmpvbvmm



Lwg徹底比較 スターリング マンチェスターシティ Vs サディオ マネ リバプール スポクラマガジン


Lindsey Stirling Youtube



フジタサチヒコ スターリングウルトラコールドストーリーだ ツインバードストーリーはこれだよ T Co 0pgexb2zjk



林俊克 廣野元久 多変量データの活用術 海文堂 Ppt Download



ヤフオク F1440 レア 1piu1uguale3 Wolf S Head 美しい



第2種スターリング数 高校生向け 1 怜悧玲瓏 高校数学を天空から俯瞰する



13 号 スターリングエンジン制御システム及びスターリングエンジン搭載船舶 Astamuse



9 23 U 9 日之出スターリング実施要項 日程


写像12相をいちから勉強してatcoderの組合せ 数え上げ問題をクリアしたいと思ったけどまだまだ知らない事が多いと強烈に感じた Ctoの日記



数学セミナー17年11月号 特集 コンピュータ将棋 囲碁のこれから ず S 将棋



第1種スターリング数と第2種スターリング数 怜悧玲瓏 高校数学を天空から俯瞰する



ヤフオク 音済百太郎 B Project 鼓動 アンビシャス Bri



場合の数24 第2種スターリング数2 怜悧玲瓏 高校数学を天空から俯瞰する



第2種スターリング数の漸化式を観察する 7 怜悧玲瓏 高校数学を天空から俯瞰する



場合の数27 第2種スターリング数5 漸化式の証明 怜悧玲瓏 高校数学を天空から俯瞰する


Kadai78



ベル数 Wikipedia
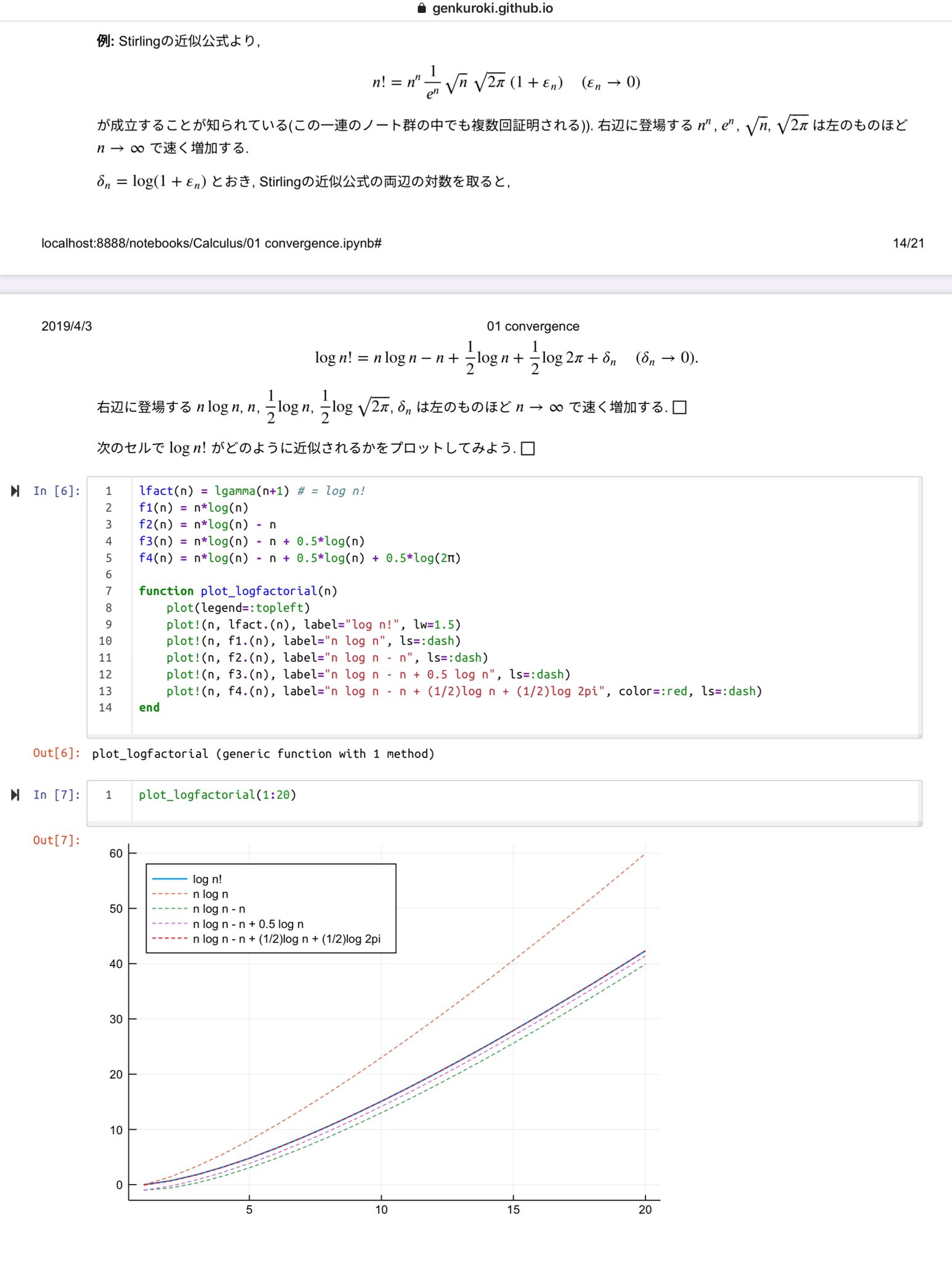


黒木玄 Gen Kuroki 数楽 階乗に関するstirlingの近似公式の対数版のプロット Log N N Log N N 1 2 Log N Log 2p O 1 添付画像2枚目の2つ目のグラフを見れば Nがものすごく大きければ Log N の N Log N による近似がそう悪くないことが



ジッポー ウィンディー スターリングシルバー ジッポー好きのオッサンのブログ



スターリングの公式の証明に関しての質問です 1枚目の最後から2行目の Clear



黒木玄 Gen Kuroki 数楽 Kl情報量sp I Log P I Q I の各項はpoisson分布から来ていたんですね スターリングの公式より E L L K K K L K E K L 2pk 右辺の分子の対数が本質的にkl情報量 続く



スターリングの標識ベクトルポンド 1ポンド硬貨のベクターアート素材や画像を多数ご用意 Istock


邑久高紀vol スターリングエンジン 10 11



Ll リサイト スターリングの通販 ねねおに Magi トレカ専用フリマアプリ



第1種スターリング数と第2種スターリング数 怜悧玲瓏 高校数学を天空から俯瞰する



場合の数46 第1種スターリング数 怜悧玲瓏 高校数学を天空から俯瞰する



13 1197号 スターリングエンジンシステム及びスターリングエンジンシステムを搭載した船舶 Astamuse



Amazon Noahバー名前ネックレス Noahバー名前ネックレススターリングシルバーincludes 18 チェーン ネックレス 通販



高校数学 アルファ スターリングの公式 Youtube



第2種スターリング数 高校生向け 2 怜悧玲瓏 高校数学を天空から俯瞰する



レミントンスターリングとは 搾取満々の案件にしか見えない件



スターリングのさらなる成長を期待するペジェグリーニ ゴール数は今までより増える ゲキサカ



ヤフオク 珍品 純銀スターリング 1929年製 卓上オイルライ



黒木玄 Gen Kuroki 数楽 第二種スターリング数 K R の定義は A K S R 0 K K R A A 1 A R 1 と同値であり A A 1 A R 1 のaに関する和は易しいので 文献を探すまでもなく 自明な結果だと思います T Co Ezuoma0tlc T Co



数学セミナー 17年 01 月号 雑誌 本 通販 Amazon


ダブルアールエル Rrl アメリカ製 スターリング シルバー マネー クリップ ハンドメイド メンズ ユニセックス Sterling Silver Money Clip Rrlmncrp19 Garyu 通販 Yahoo ショッピング



第2種スターリング数の漸化式を観察する 3 怜悧玲瓏 高校数学を天空から俯瞰する



メルカリ ソウルスターリング メンズ 1 000 中古や未使用のフリマ



コスモスターリング Cosmo Sterling 牡 4歳 中央競馬 登録抹消 サラブレッドオークション


スターリングハウストラスト プライベートバンク その3



0 件のコメント:
コメントを投稿